Learn It

Look at the graphs below. All of the functions graphed are altered versions of one parent function, f of x equals x squared. This parent function f of x equals x squared has been transformed to form the eight other functions.

Nine graphs displaying different parabolas are shown. In each graph, both the x and y axes extend from negative 10 to 10, with the x axis labeled with an x and the y axis labeled as f of x. Graph 1 shows the parent function f of x equals x squared, which is a parabola opening up with a vertex at the origin. Graph 2 shows the graph of a parabola opening up whose vertex is at the point (0, 5). Graph 3 shows the graph of a parabola opening up whose vertex is at the point (0, negative 3). Graph 4 shows the graph of a very skinny parabola opening up whose vertex is at the point (0, 0). Graph 5 shows the graph of a very wide parabola opening down whose vertex is at the point (0, 0). Graph 6 shows the graph of a parabola opening down whose vertex is at the point (4, 5) and crosses the x axis at x equals 2 and x equals 6. Graph 7 shows the graph of a very wide parabola opening up whose vertex is at the point (0, 0). Graph 8 shows the graph of a parabola opening up whose vertex is at the point (negative 5, 0). Graph 9 shows the graph of a parabola opening up whose vertex is at the point (4, 0).

Functions can be modeled in the xy-coordinate plane. By transforming the equation of a function, the graph of the function can be transformed about the plane.

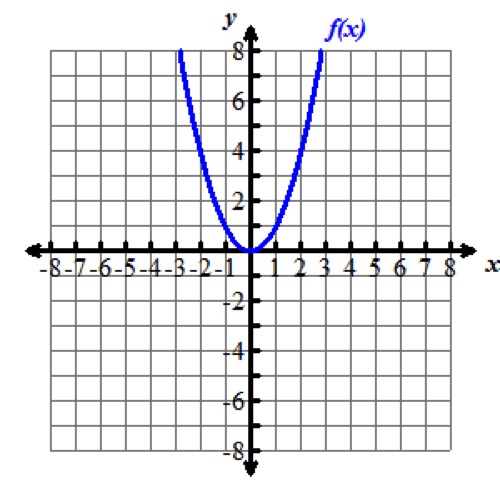
f of x equals x squared A graph showing the parent function f of x equals x squared, which is a parabola opening up with a vertex at the origin. In the graph, both the x and y axes extend from negative 10 to 10, with the x axis labeled with an x and the y axis labeled as f of x.
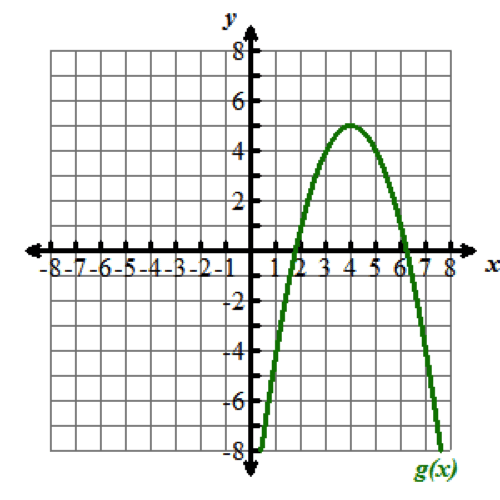
g of x equals negative f of x minus 4 plus 5 A graph showing the graph of the function g of x, which is a parabola opening down, crosses the x axis at x equals 2 and x equals 6, with a vertex at the point (4, 5). In the graph, both the x and y axes extend from negative10 to 10, with the x axis labeled with an x and the y axis labeled as g of x.

Explore the following videos to learn how functions are transformed in the xy-coordinate plane.

Transformation: f of x plus k

Watch the following video to see how the function f of x is transformed by adding a value of k to the function. That is, f of x plus k.

This video player plays a video on transformation.

> Text version for video: Transformation: f(x)+k Opens a new window


f of x plus k

Adding a value of k to a function f of x translates the graph up vertically when k is positive and down vertically when k is negative.

Transformation: f of the quantity x plus k

Now let’s examine the effects of adding a value of k to the domain (x) of f of x, forming the function f(x+k)f of the quantity x plus k.

Before you watch the video, do you have any predictions about how the function may be transformed?

Watch the following video to see if you are correct.

This video player plays a video on transformation.

> Text version for video: Transformation: f(x+k) Opens a new window


f of the quantity x plus k

Adding a value of k to the domain of the function f of x translates the graph of the function left horizontally k units when k is positive and right horizontally when k is negative.

Transformation: kf(x)

Now watch the following video to see how the function f(x) is transformed by multiplying a value of k by the function. That is, kf(x).

This video player plays a video on transformation.

> Text version for video: Transformation: kf(x) Opens a new window


k times f of x

When a function f of x is quadratic or exponential, multiplying by k will dilate the function for large values of k and reduce the function for small, positive values of k.

For linear functions, multiplying by k will increase the slope of the line for large values of k and decrease the slope of the line for small, positive values of k.

negative f of x

When k is negative, the function is reflected, or flipped, in the x-axis.

Transformation: f of the product of k and x

We have one more transformation to examine. Watch the following video to see how the function f of x is transformed by multiplying a value of k to the domain (x) of the function. That is, f of the product of k and x.

This video player plays a video on transformation.

> Text version for video: Transformation: f(kx) Opens a new window


f of the product of k and x

When the function f of x is a quadratic function, multiplying a value of k to the domain (x) of the function will dilate (or stretch) the parabola for small, positive values of k and reduce (or shrink) the function for large values of k.

For exponential functions, multiplying a value of k to the domain (x) of the function will dilate (or stretch) the curve for small, positive values of k and reduce (or shrink) the curve for large values of k.

For linear functions, multiplying the domain by k will increase the slope of the line for large values of k and decrease the slope of the line for small values of k.

f of negative x

When k is negative, the line is reflected (or flipped) in the y-axis.