Try It
The factored form of a quadratic function reveals the zeros of the function, while the vertex form of a quadratic function reveals the maximum or minimum of the function. The value of converting quadratic functions in these representations can be appreciated when the function is applied to a real-world situation. Be sure to use your graphing calculator as you work through the following activities.
Legend says that there are pots of gold at the end of rainbows. Have you ever gone looking for one? Here is a picture of a rainbow.

The rainbow is superimposed onto a coordinate grid. Notice how it models a quadratic function.
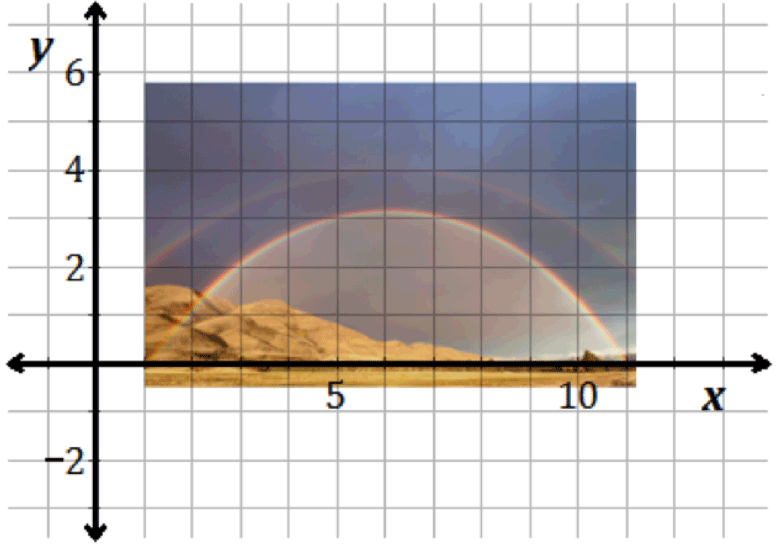
Note: The quadratic function h of x is equal to negative one eighth times x squared plus three halves x minus eleven eighths can be used to represent the curve of the rainbow.
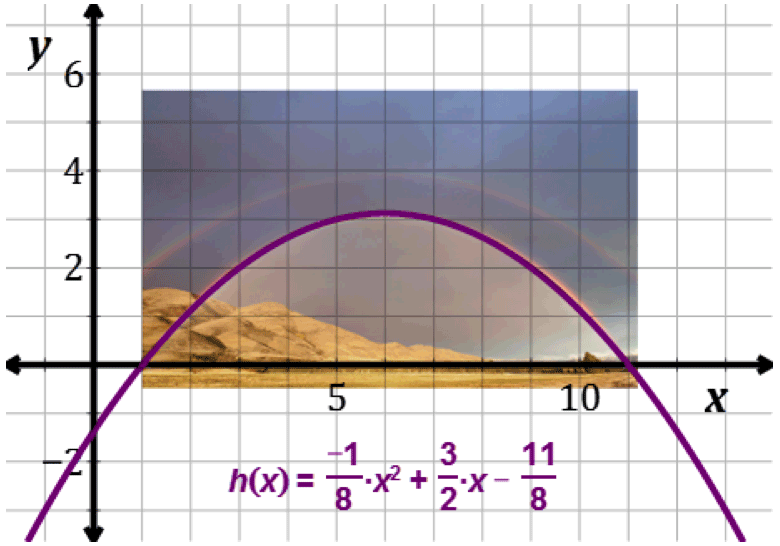
The “pot of gold at the end of the rainbow” would be located at the zeros of the quadratic function.
Complete the interactive below to answer questions about the function above.
Tip
Vertex form of a quadratic function is written in the form y equals a times the quantity x minus h squared plus k. The vertex of the parabola is (h,k).
Factored form of a quadratic function is written in the form y equals a times the quantity x minus m times the quantity x minus n. The zeros of the function are m and n.


