Sequences as Functions

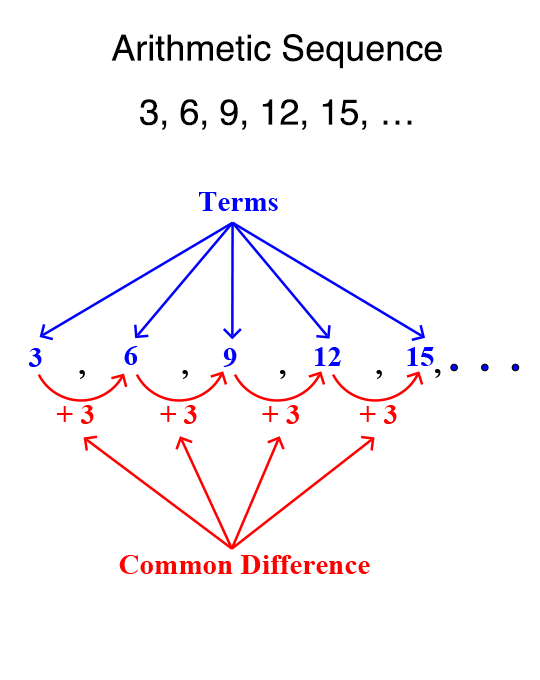
An arithmetic sequence is a numerical pattern in which the difference between consecutive terms is constant. This constant is called the common difference. Terms are the values of numbers in the sequence. Each term is equal to the sum of the term before it plus the common difference. Terms increase at a constant rate when the common difference is positive. They decrease at a constant rate when the common difference is negative.

The common difference is used to extend the sequence. The common difference is the value that is added or subtracted from each term in an arithmetic sequence in order to generate consecutive terms. The common difference is typically represented by the variable “d.” In this sequence, the common difference is +3.

In general, arithmetic sequences can be described as follows:

a₁a sub 1, a₂a sub 2, a₃a sub 3, a₄a sub 4, a₅a sub 5, and so on, where d represents the common difference and a_n represents the terms in the sequence.

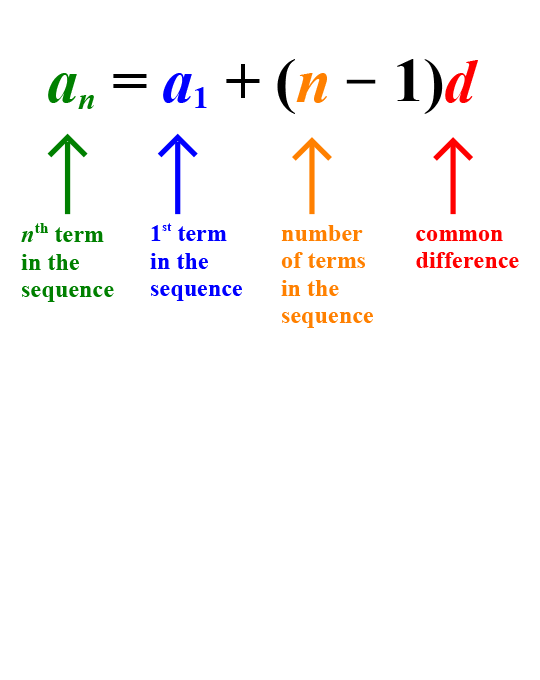
The value of the nth term of an arithmetic sequence can be determined by applying the formula: a_n = a₁+(n - 1)timesdA sub n equals a sub 1 plus the quantity n minus 1 times d. This formula is the explicit formula for finding the nth term of an arithmetic sequence.

For the sequence we looked at earlier, the explicit formula for any term n in this sequence would be

a_n = 3 + (n - 1)times(3)A sub n equals 3 plus the quantity n minus 1 times 3

This example illustrates how to use the explicit formula to determine the value of the 8^th term in the given sequence. Since the sequence has been extended to show that the value of the 8th term is 24, we are able to verify that this formula produces the correct value.

The explicit formula

a_n = a₁ + (n - 1)timesdA sub n equals a sub 1 plus the quantity n minus 1 times d

can be used to find the value of any term in an arithmetic sequence. To use this formula the value of the first term in the sequence is substituted in for a₁, the value of the common difference is substituted in for “d” and the letter “n” is replaced with the desired term's location in the sequence.

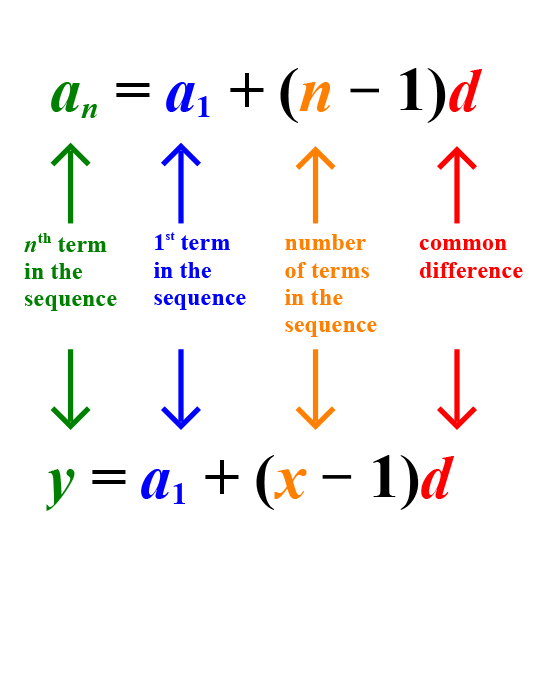
An arithmetic sequence is actually a linear function whose domain is the set of positive integers. Both linear functions and arithmetic functions are connected by the idea of “common difference.” The steps in the illustration demonstrate how the formula for the nth term of an arithmetic sequence can be manipulated to resemble the slope intercept form for a linear function.

When y = a₁ + (x - 1)timesdY equals a sub 1 plus the quantity x minus 1 times d. is further simplified to y = dx + (a₁ - d)Y equals d x plus the quantity a sub 1 minus d, the arithmetic formula resembles the slope-intercept formula for linear equations, y = mx + b. The slope, m, is equivalent to the common difference, d, of the arithmetic sequence. The y–intercept is equivalent to the first term in the sequence, a_n minus the common difference, d. In other words, the value of b is equal to the quantity a₁ - d.a sub 1 minus d
This is why arithmetic sequences are linear functions!

For the pattern we looked at earlier, we arrived at the general formula:

a_n = 3 + (n - 1)times(3)A sub n equals 3 plus the quantity n minus 1 times 3

This formula can be rewritten as a linear function.

So, for example, if we substitute 8 in for x, we get y = 24. Recall that the eighth term in the sequence was 24!

Linear functions form lines when graphed. You can use your graphing calculator to check this.

In the graph shown, the points correspond to the points in the sequence.

The arithmetic sequence, which is a linear function, forms the straight line because of the common difference. For every increase of one term in the pattern, the value of the term increases by 3.

Here is another example of an arithmetic pattern.

This pattern is arithmetic because it adds a common difference of -negative1.5. (You can also think of this as subtracting 1.5.)

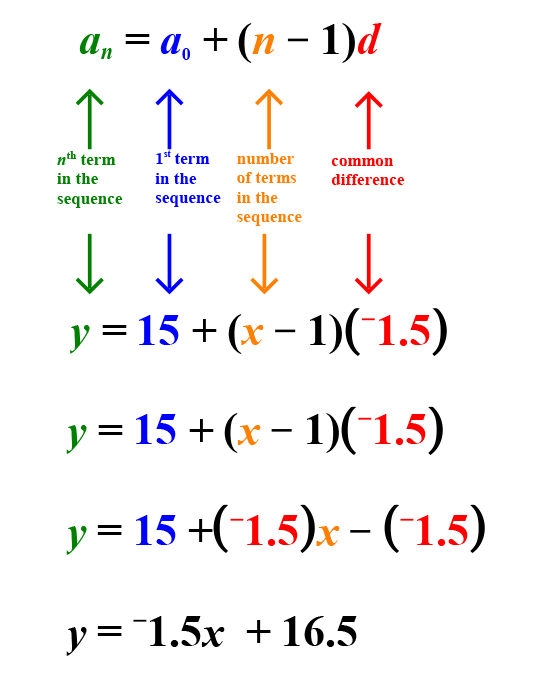
The explicit formula to represent this arithmetic sequence can be written as
y = -negative1.5x + 16.5

Here is the arithmetic sequence graphed as the linear equation,
y = -negative1.5x + 16.5

The y-value of each point shown on the line is a value in the sequence.

The common difference of -negative1.5 ensures the linear relationship.