Sequences as Functions

Here is an example of a geometric sequence.

Geometric sequences are numerical patterns in which each term after the nonzero first term is determined by multiplying the previous term by a constant factor, known as the common ratio. The terms in a geometric sequence increase when the factor is greater than 1. The terms decrease when the factor is between 0 and 1.

In a geometric sequence, the common ratio is the fractional value of any given term compared to its preceding term in the sequence. In the fraction, the given term is the numerator and its preceding term is the denominator.

In this example, the common ratio is 3 because ==== 3nine thirds equals twenty seven ninths equals eighty one twenty sevenths equals two hundred forty three eighty firsts equals three. Thus, to extend the pattern, multiply each term by 3 to produce the next term.

In general, geometric sequences can be described as shown, where “r” represents the common ratio and a_na sub n represents a term in the sequence.

Specific terms in a geometric sequence can be found by using the formula shown.

For the pattern we looked at earlier, the first term was 3 and the common ratio was also 3. The illustration shows how to determine the value of the 8^th term by using this formula:

a_n = 3 times⋅ 3 ^{(n - 1)}a sub n equals 3 times 3 to the power of n minus 1

As you can see, the 8th term in this pattern is 6561. Examine how to use the formula to find the 8th term.

The explicit formula for the nth term of a geometric sequence is
a_n = a₁times⋅ r^{(n - 1)}a sub n equals a sub 1 times r to the power n minus 1. This formula is used to find the value of a desired term of a geometric sequence. Simply substitute the value for the first term, a₁a sub 1, the value of the common difference “r” and the value of the placement of the desired term, n, in the formula. Simplify to determine the value for that n^th term.

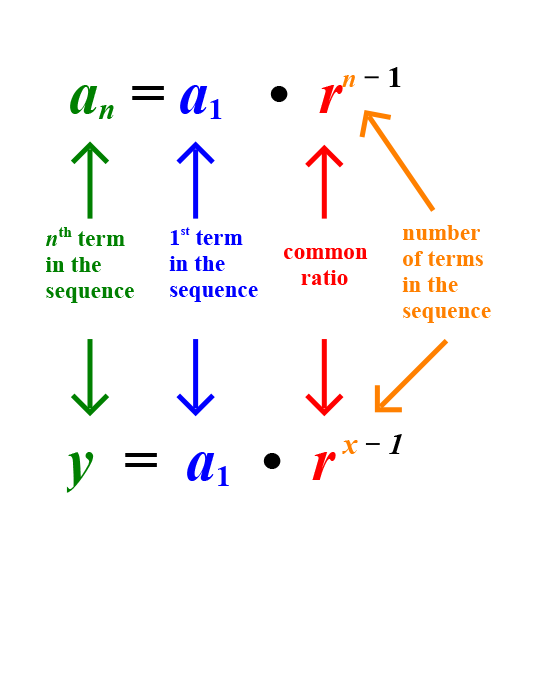
A geometric sequence is actually an exponential function whose domain is the set of positive integers. Geometric sequences and exponential functions are connected by the idea of a common ratio or common multiplier. The steps in the illustration demonstrate how the formula for the nth term of a geometric sequence can be manipulated to resemble the general form of an exponential function.

When y = a₁times⋅ r^{x - 1}y equals a sub 1 times r to the power x minus 1 is further simplified to y = a₁times⋅ b^xy equals a times b to the power x, the geometric formula resembles the general form for exponential equations, y = atimes⋅ b^x. The actual steps in this transformation are a little tricky. The next example may be easier to follow.

For the pattern we looked at earlier, we arrived at the general formula:

a_n = 3 times⋅ 3 ^{(n - 1)}a sub n equals 3 times 3 to the power n minus 1

This formula can be rewritten as an exponential function.

So, for example, if we substitute 8 in for x, we get y = 3⁸ = 6561y equals 3 to the power eight equals six thousand five hundred sixty one. Recall that the eighth term in the arithmetic sequence was 24!

Exponential functions form exponential curves when graphed. You can use your graphing calculator to check this for y = 3^xy equals 3 to the power x.

In the graph shown, the points correspond to the points in the sequence. The geometric sequence, which is an exponential function, forms the exponential curve because of the common ratio.

For every increase of one term in the pattern, the value of the term increases by a factor of 3.

Here is another example of a geometric pattern.

This pattern is geometric because it multiplies by a common ratio of . (You can also think of this as dividing by 3.)

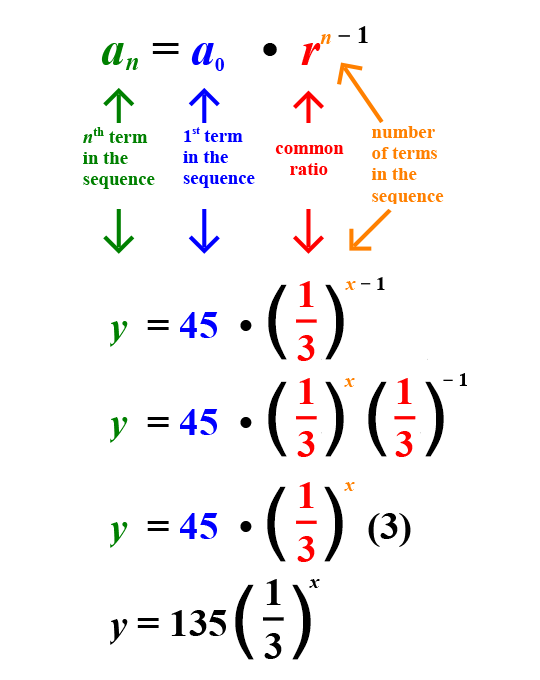
The explicit formula to represent this geometric sequence can be written as .

Here is the geometric sequence graphed as the exponential equation, .

This is exponential decay.

The y-value of each point shown on the line is a value in the sequence.

The common ratio of ensures the exponential relationship.