This module is for Algebra 1, Grades 7-12 Welcome
On February 8, 2015, the population of the United States was approximately 320,304,889 people. Check the population of the United States today at Census.gov Opens a new window. How much has the population increased? How many people will be in the United States five years from today? How can we determine that?
The temperature forecasted for one day in February is shown below.
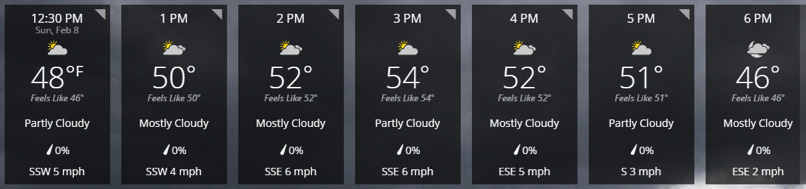
Source: http://www.weather.com/weather/hourbyhour/l/21236:4:US
What do you think the actual temperature was at 7 p.m.? Consider the temperatures in your neighborhood as you complete this module. What will the temperatures be tonight? How can you predict this?
These examples are just two real-world scenarios that can be analyzed mathematically. We can determine an equation (a function) to model each one of these situations, and we can use the equations to extrapolate or to interpolate data. In this module, you will learn how to determine an equation that best represents a given set of data and to use that equation to solve problems.
Module Objective
By the end of this module, you will be able to:
- Perform linear, exponential and quadratic regressions.
- Analyze the fit of a regression line/curve using correlation coefficients and the coefficient of determination.
Skills
- Recognize linear, quadratic and exponential patterns displayed in data.
- Use the graphing calculator to calculate the appropriate regression curve for a set of data.
- Identify the curve of best fit using the correlation coefficient and/or the coefficient of determination as justification.
- Use the regression curve to interpolate and to extrapolate data.
- Interpret slope (for linear models), intercepts, and average rates of change for regression curves to solve problems in context with data.








