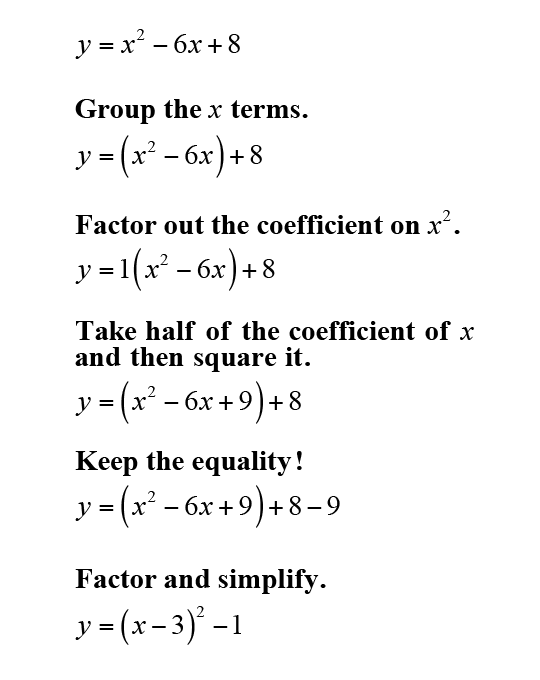Skip to main content

Learn It

Which of the following forms of a quadratic equation is easier for you to read and understand?

  1. y=x2−6+2x+2(4x2)−6x+3−23x2+11−2x
  2. y=x2−6x+8

In mathematics, we find that certain forms of equations can make our work easier, even when the different forms represent the same equations. In this lesson, we will focus on the standard form and on the vertex form.

Standard form of a quadratic function is written as y=ax2+bx+c. This form is useful when evaluating a function for different values of x. Also, standard form is easy to graph by hand or by entering into a graphing calculator because the equation already is written as “y=”. Take a look at the example below:

The quadratic equation y=x2−6x+8 is written in standard form. Graph this function in your graphing calculator. Your graph should be similar to the one shown on the right.

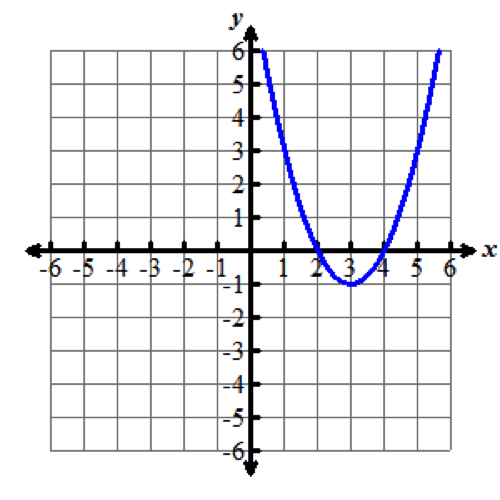
a coordinate grid with x and y axes extending from -6 to 6, in increments of 1. A parabola is graphed. The parabola opens up, crosses the x-axis at 2 and 4, and has a minimum at the point (3, -1).

The vertex form of a quadratic equation emphasizes the exact location of the vertex of the parabola. This form of a quadratic equation is significant because the vertex of a parabola is the maximum or minimum point of the parabola, and represents the maximum or minimum value of the quadratic equation. The vertex form also helps us solve for the exact roots, or zeros, of the quadratic equation. Later in the module, you will learn to change a quadratic function written in standard form to its vertex form.

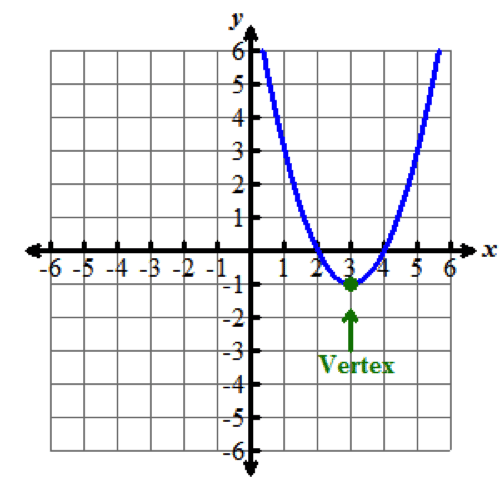
The vertex form of a quadratic function for this equation is written as y=(x−3)2−1.

You may be wondering why we must be able to find the vertex and zeros of a quadratic function by hand when the calculator gives us these answers so easily. Solving for the vertex and zeros by hand will produce the exact values. When the zeros and the vertex are irrational or decimal values, the calculator provides only rounded, or approximate, answers.

The vertex of this parabola is (3,negative1).

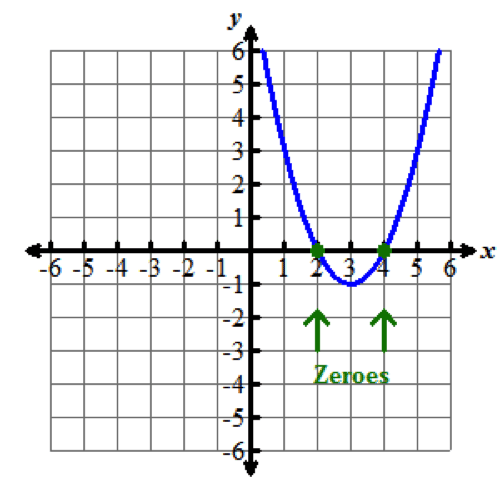
The graph of the same parabola is shown, with arrows pointing at where the parabola crosses the x-axis. These points (2, 0) and (4, 0) are identified as the zeroes of the parabola.

If we set this equation equal to zero, we can find the exact zeros (or solutions) to the quadratic equation.

Y equals the quantity x minus three squared minus one the quantity x minus three squared minus one equals zero the quantity x minus three squared equals one the square root of the quantity x minus three squared equals plus or minus the square root of one x minus three equals plus or minus one x equals three plus or minus one x equals 2 and 4

The graph of the same parabola is shown, with arrows pointing at where the parabola crosses the x-axis. These points (2, 0) and (4, 0) are identified as the zeroes of the parabola.

How can we rewrite a quadratic equation given in standard form as an equivalent equation in vertex form, without having to graph the equation? The following slideshow will take you through the steps of completing the square, a process that will change a quadratic equation into vertex form and help solve for the roots of the quadratic equation.

Speaker plays audio

Completing the Square

A quadratic equation takes the standard form
y equals a x squared plus b times x plus c.

The first step in completing the square is to group the x terms together.

Now, factor out the coefficient of the xsquared term.

Take half of the coefficient of the x term and then square it.

Add this value to the terms in the parentheses.

This forms a perfect square trinomial.

Keep the equality of the equation by taking the value added in Step 3, and subtracting it.

Be careful because the value added in Step 3 is the product of the coefficient we factored out in Step 2 and the value added in the parentheses.

That is, a times the quantity 1 b squared divided by the quantity 4 a squared or the quantity 1 b squared divided by 4 a.

Factor the perfect square trinomial.

Voila! You now have transformed the quadratic equation into vertex form!

Here is how to rewrite y equals x squared minus 6 x plus 8 into vertex form by following the steps to complete the square.

The vertex is (3,negative1).