Skip to main content

Learn It

Hermione is starting her own business, Cupcakes and Cake-Ups Bakery. She and her staff can make at most 800 cupcakes and 600 cakes in one day. Her current bakery is small and therefore can hold 1,000 cupcakes and cakes altogether. Hermione sells each cupcake at a price point that gives her a $2.00 profit and each cake at a price point that gives her a $7.50 profit. Hermione wants to maximize her profits each day while avoiding waste.

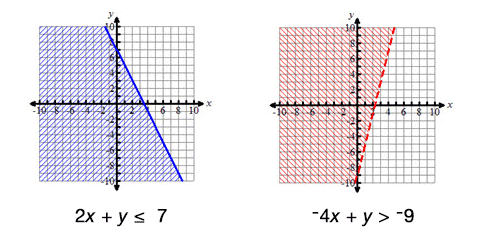
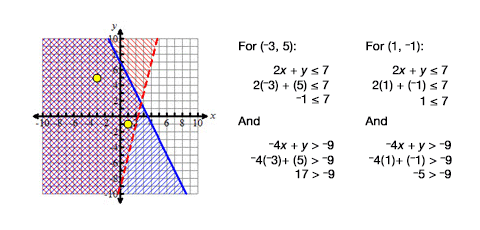
How many cupcakes and cakes should she sell to maximize her profits? What can you use to solve this problem? The process of writing and graphing linear inequalities can be used to help solve problems like this.

cupcakes being decorated by hands

View the following slideshow to build an understanding of solving linear inequalities.

Speaker plays audio

Linear Programming

These are graphs of various linear inequalities.
The graph on the left shows the linear inequality 2x + y ≤ 7.
The graph on the right shows the linear inequality negative4x + y > negative9.

The shaded region of a linear inequality represents all possible solutions (x, y) to the inequality.
The yellow dots in the shaded regions show some of these solutions.
If the linear inequality uses a solid line, like the graph on the left, the line also represents possible solutions.

Shown here on this graph, points (negative4, 5), (5, negative3) and (0, 0) are solutions to the inequality 2x + y ≤ 7.

And on this graph, points (negative6, negative4), (1, 5) and (0, 0) are solutions to the inequality negative4x + y > negative9.

A system of linear inequalities is a set of linear inequalities graphed on the same coordinate plane.

The coordinate pairs (x, y) that fall within the common shaded region are solutions to all the linear inequalities in the system. The two dots shown on this graph are examples of such coordinate pairs.

Some solutions are significant. For example, the point where the two lines cross in the system may be of significance. The points where the lines cross the axes may be of significance. When a system of linear inequalities models a real-world situation, these significant solutions become critical to identify.


Now go to the next page to see how the real-world bakery example can be modeled by a system of linear inequalities.