Learn It Part 2
Let’s take a closer look at arithmetic sequences and geometric sequences. Suppose strands of a new, unknown virus have entered the United States. The Centers for Disease Control and Prevention (CDC) are monitoring the growth of the virus. The CDC determines that one strand of the virus, identified as Strand A, grows arithmetically with a common difference of 11. The CDC determines the other strand, identified as Strand B, grows geometrically with a common ratio of 1.11.
Complete the pattern below, showing the number of people who contract the strands of the virus. You may print a copy of the tables Opens a new window, or copy each table onto a separate sheet of paper to complete this activity. Round any decimals to the thousandths place. When you are done, click the Show Answer button to check your work.
Strand A
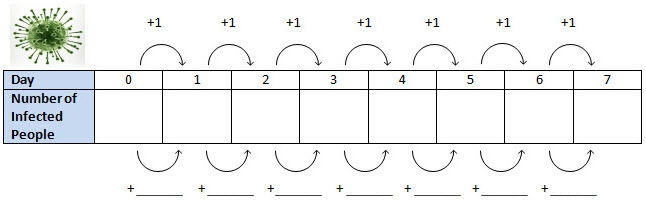
Strand B
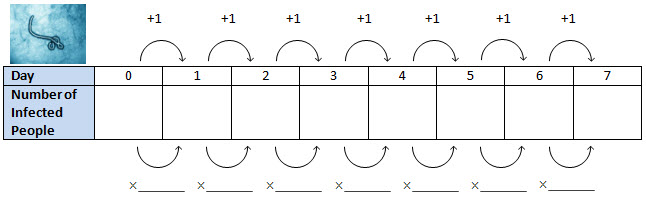
Tip
Strand B grows by 11%. The common ratio is 1.11 because it takes into account the number of people previously infected by the virus.
The Strand A virus follows an arithmetic sequence because it follows an additive pattern. The common difference is 11. Choose a term in the pattern and subtract the previous term, and you will get this common difference.
Did you recognize the Strand B virus? This is the Ebola virus that entered the United States in 2014.
The Ebola virus is an example of a geometric sequence because it follows a multiplicative pattern. The common ratio is 1.11. Choose a term in the pattern and divide the previous term, and you will get this common ratio.
The Ebola virus has many scientists worried because it spreads very quickly. It may not appear to be too threatening in the tables you just completed, but if you extend the tables past sixty days, the growth of the Ebola virus greatly overtakes the growth of Strand A.
Strand A

Strand B





