Click each step to learn more.
Step 1: Analyze the pieces of the function.Example:
f(x)=
-negative9,x<-negative2
3,-negative2≤x≤4
9,x>4
All the pieces of this function are constant linear functions. Therefore, this piecewise function is a step function.
f(x)=
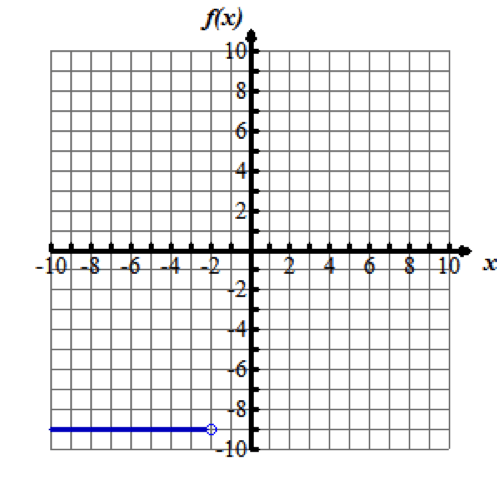
-negative9,x<-negative2 ![]() This step has the value of -negative9 over the domain -negative∞ to -negative2.
This step has the value of -negative9 over the domain -negative∞ to -negative2.
3,-negative2≤x≤4
9,x>4
f(x)=
-negative9,x<-negative2 ![]() This step has the value of -negative9 over the domain -negative∞ to -negative2.
This step has the value of -negative9 over the domain -negative∞ to -negative2.
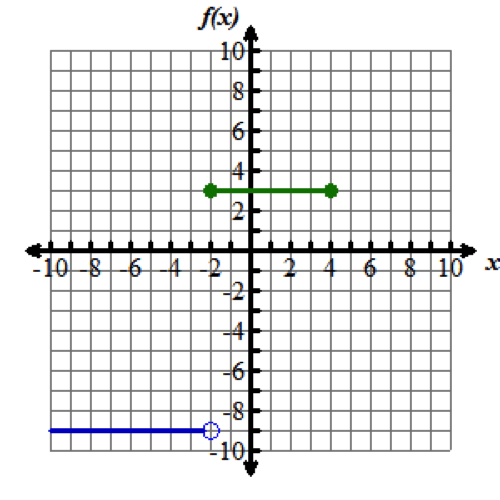
3,-negative2≤x≤4 ![]() This step has the value of 3 over the domain -negative2 to 4, inclusive.
This step has the value of 3 over the domain -negative2 to 4, inclusive.
9,x>4
f(x)=
-negative9,x<-negative2 ![]() This step has the value of -negative9 over the domain -negative∞ to -negative2.
This step has the value of -negative9 over the domain -negative∞ to -negative2.
3,-negative2≤x≤4 ![]() This step has the value of 3 over the domain -negative2 to 4, inclusive.
This step has the value of 3 over the domain -negative2 to 4, inclusive.
9,x>4 ![]() This step has the value of 9 over the domain 4 to +∞.
This step has the value of 9 over the domain 4 to +∞.
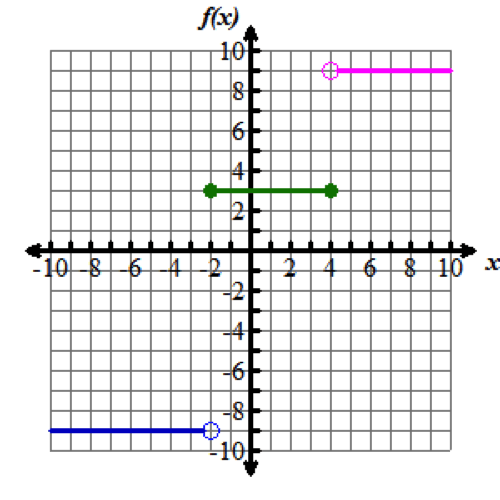
Our example only has three pieces, so the graph is complete. Some step functions can have many steps.
f(x)=
-negative9,x<-negative2 ![]() This step has the value of -negative9 over the domain -negative∞ to -negative2.
This step has the value of -negative9 over the domain -negative∞ to -negative2.
3,-negative2≤x≤4 ![]() This step has the value of 3 over the domain -negative2 to 4, inclusive.
This step has the value of 3 over the domain -negative2 to 4, inclusive.
9,x>4 ![]() This step has the value of 9 over the domain 4 to +∞.
This step has the value of 9 over the domain 4 to +∞.

The vertical difference between the function x<-negative2x is less than negative 2 and the function -negative2≤x≤4x is greater than or equal to 2 and less than or equal to 4 is 12 units, from y=-negative9 to y=3.
The vertical difference between the function -negative2≤x≤4x is greater than or equal to 2 and less than or equal to 4 and the function x>4x is greater than 4 is only 6 units, from y=3 to y=9. Thus, the vertical distances between the steps do not need to be uniform, as in the example for the “round up” program.