The Real Number System

Look again at these numbers.

• 8
• -negative4
• √2the square root of 2
• 23two thirds
• 0.111zero and one hundred eleven thousandths repeated
• 0
• πpi
• -negative82eight halves

Each of these numbers is unique in its design and has special characteristics. Some of these numbers have common properties, while others are unique.

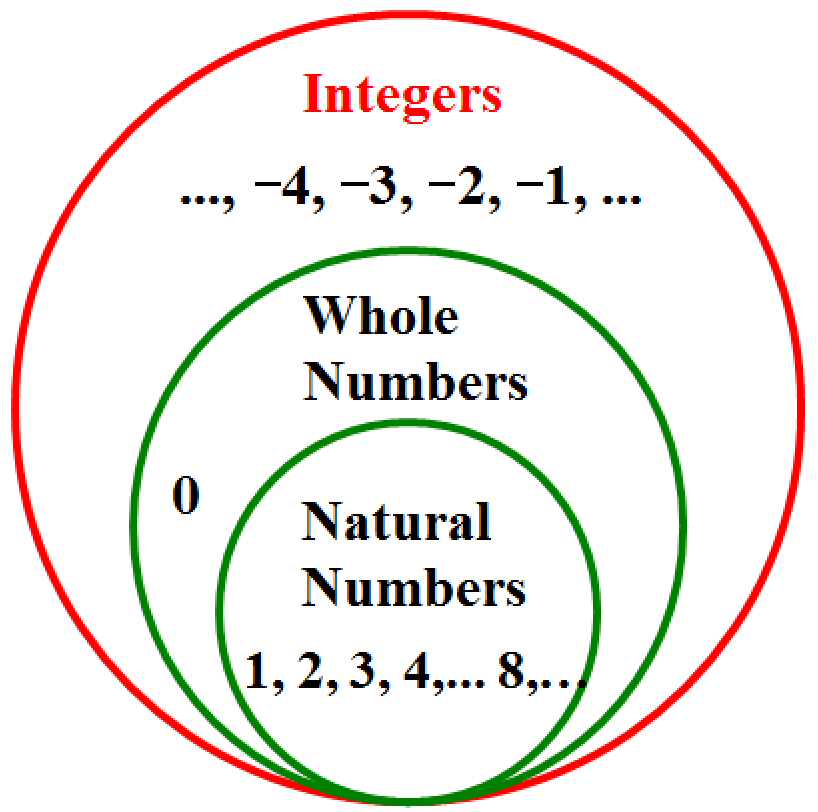
The counting numbers, or whole numbers, are known as the natural numbers. These are the numbers 1, 2, 3, 4, 5, 6, 7, 8, and so on.

Whole numbers combine the set of natural numbers with zero (0). These are the numbers 0, 1, 2, 3, and so on.

For example, 0 and 8 are whole numbers.

The integers include the natural numbers, zero (or the whole numbers), and the negative counting numbers (the opposite of the whole numbers): … -negative4, -negative3, -negative2, -negative1, 0, 1, 2, 3, 4, and so on.

Integers have no fractional parts.

For example, -negative4, 0 and 8 are integers.

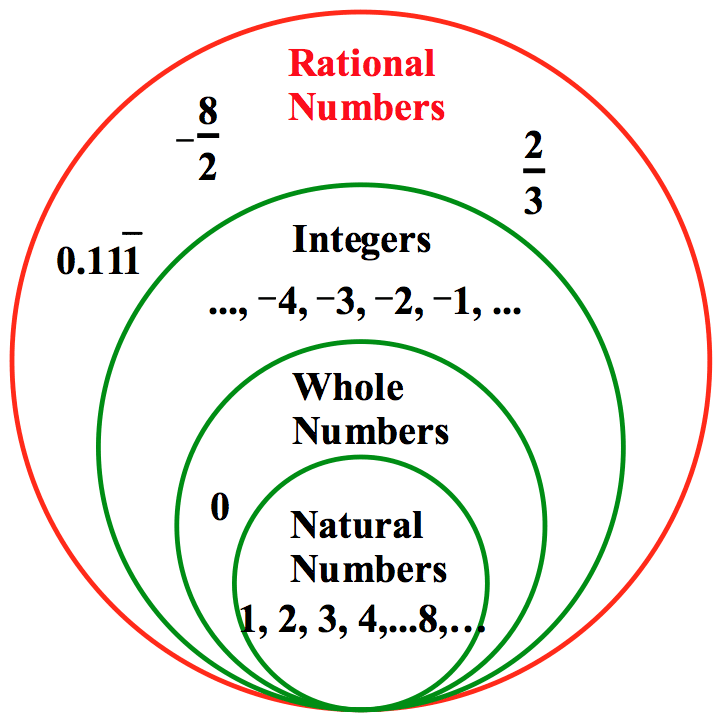
The rational numbers are the numbers that can be made by dividing one integer by another integer.

A rational number is a number that can be written in the form aba divided by b, where a and b are integers and b≠0b is not equal to zero. -negative82eight halves and 23two thirds are rational numbers.

0.111zero and one hundred eleven thousandths repeated is a rational number because it can be rewritten as 19one ninth. Rational numbers include terminating decimals (such as -negative4.0) and repeating decimals (such as 0.111zero and one hundred eleven thousandths repeated).

-negative4, 0 and 8 are rational numbers because they can be rewritten as -negative41four over one, 01zero over one, and 81eight over one, respectively. Therefore, the set of rational numbers includes all the integers (which are comprised of the whole numbers and the natural numbers).

Irrational numbers are numbers that cannot be written as a simple fraction.

In other words, irrational numbers are decimal values that go on forever without a repeating pattern of digits. They are numbers that cannot be represented as terminating or repeating decimals. As shown in the diagram below, irrational numbers sit apart from the set of rational numbers.

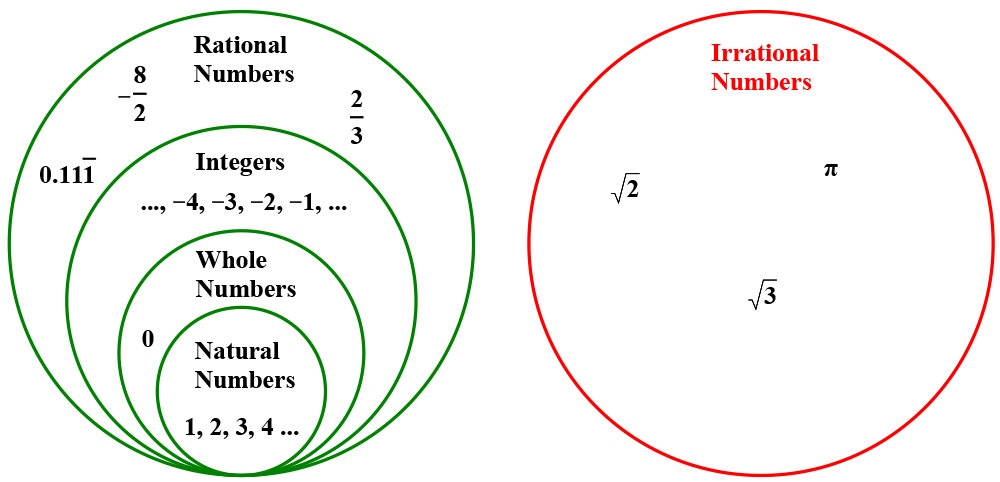
Examples of irrational numbers include π (“pi”, ≈3.1415926535…)pi, which equals 3 point one four one five nine two six five three five etc. and √2square root of 2 (≈1.414213562…)the square root of two which equals one point four one four two one three five six two etc..

The set of rational numbers combined with the set of irrational numbers form the real number system.

Also, a “non-real,” or imaginary number system exists. You will learn about this number system in a later mathematics course.