Click on a box to explore each topic.
Standard FormStandard form: y=ax2+bx+cy equals a times x squared plus b times x plus c
Example: y=2x2+4x−6y equals two times x squared plus four times x minus six
From the standard form, we know a=2, b=4, and c=-negative6.
Here is the graph of this quadratic equation:
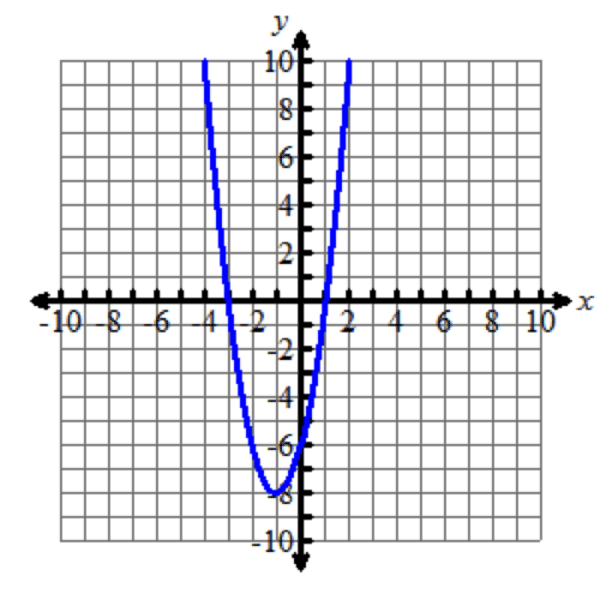
Factored form: y=a(x−m)(x−n)Factored form is y equals a times the quantity x minus m times the quantity x minus n.
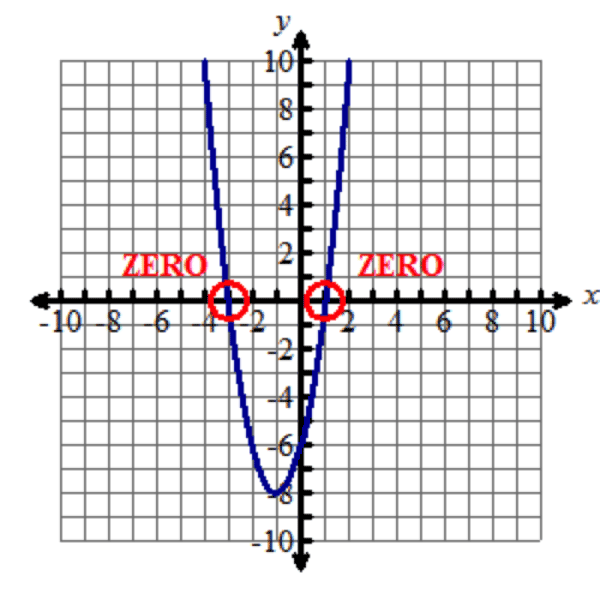
The zeros of the function y=2x2+4x−6 are -negative3 and 1. This can be seen in the graph where the parabola crosses the x–axis. This means m=-negative3 and n=1. Note that a=2, which comes from the standard form (the coefficient of the x2x squared term).
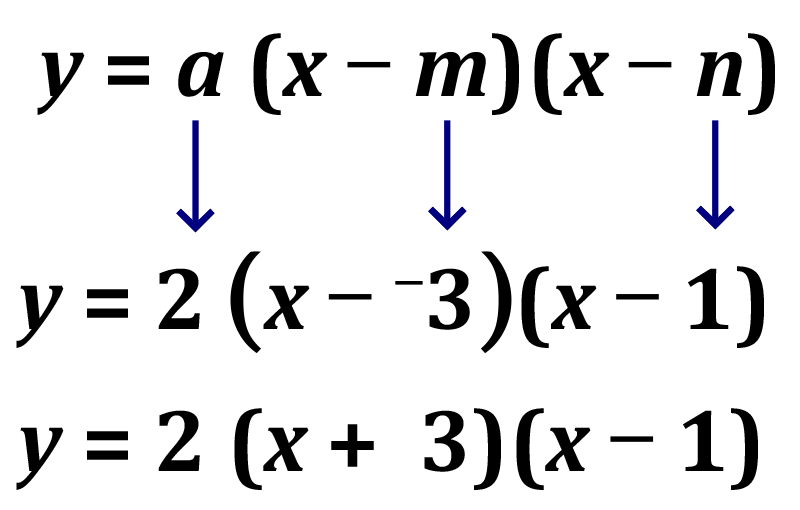
f(x)f of x can therefore be rewritten in factored form as y=2(x+3)(x−1).y equals two times the quantity x plus three times the quantity x minus one
Factored form emphasizes the zeros of the quadratic function.
Vertex form: y=a(x−h)2+kVertex form is y equals a times the quantity x minus h squared plus k.
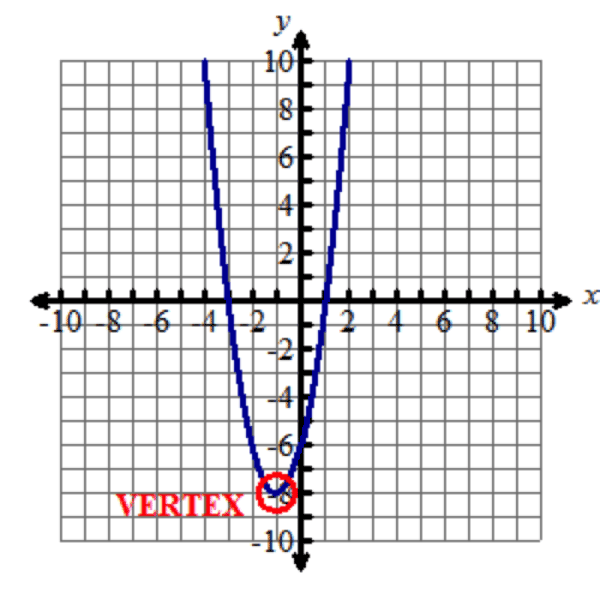
The vertex of the function y=2x2+4x−6y equals two times x squared plus four x minus six is the point negative one comma negative eight is (-negative1,-negative8). This can be seen in the graph as the minimum point of the parabola. The general form for a vertex is (h,k), so this means h=-negative1 and k=-negative8 for this parabola. Note that a=2, which the standard form gave us.
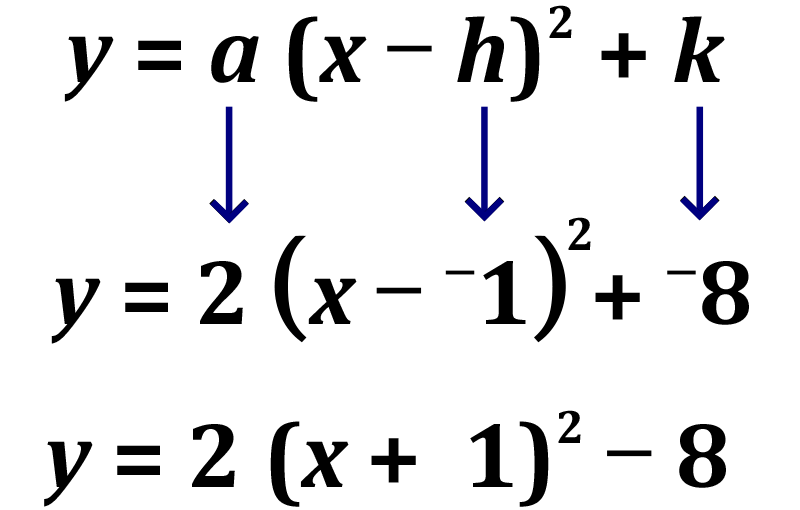
f(x)f of x can therefore be rewritten in vertex form as y=2(x+1)2−8y equals two times the quantity x plus one squared minus eight.
Vertex form emphasizes the vertex of the quadratic function.
The factored form of a quadratic function reveals the zeros of the function, while the vertex form of a quadratic function reveals the maximum or minimum (the vertex) of the function.
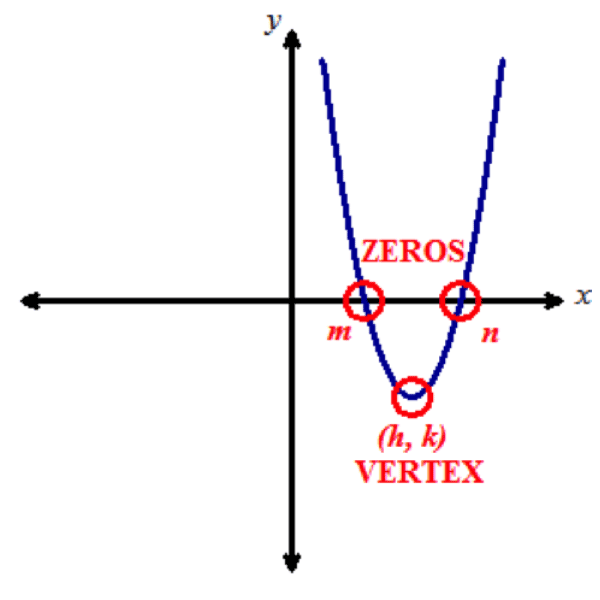
Standard form: y=ax2+bx+cStandard form is y equals a times x squared plus b times x plus c.
Factored form: y=a(x−m)(x−n)Factored form is y equals a times the quantity x minus m times the quantity x minus n.
Vertex form: y=a(x−h)2+kvertex form is y equals a times the quantity x minus h squared plus k