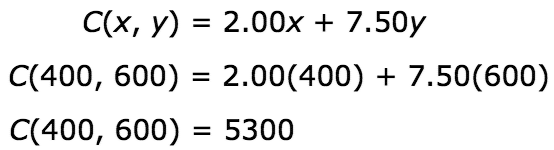Click on a box to explore each topic.
Step 1: Identify the unknowns and assign variables to them.Use x and y as the variables for modeling Hermione’s bakery scenario, where x represents the number of cupcakes she sells in one day and y represents the number of cakes she sells.
Step 2: Write the objective function (also known as the optimizing function).The objective function is the equation that is used to find the maximum or minimum value in a linear inequality situation.
Remember, Hermione sells each cupcake for a $2.00 profit and each cake for a $7.50 profit. The total profit, in dollars, is represented by the objective function, C(x, y)C of x comma y.
Objective function:
C(x, y) = 2.00x + 7.50yC of x comma y equals 2x plus 7 and five tenths y
Where x represents the number of cupcakes sold and y represents the number of cakes sold, and C(x, y)C of x comma y represents the function that optimizes the profit.The following system of linear inequalities can model Hermione’s bakery scenario, where x represents the number of cupcakes she sells in one day, and y represents the number of cakes she sells in one day.
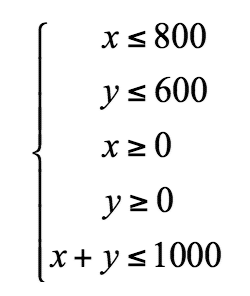
- The inequality x ≤ 800x is less than or equal to 800 comes from knowing Hermione and her staff can make, at most, 800 cupcakes.
- The inequality y ≤ 600y is less than or equal to 600 comes from knowing the bakers can make, at most, 600 cakes in one day.
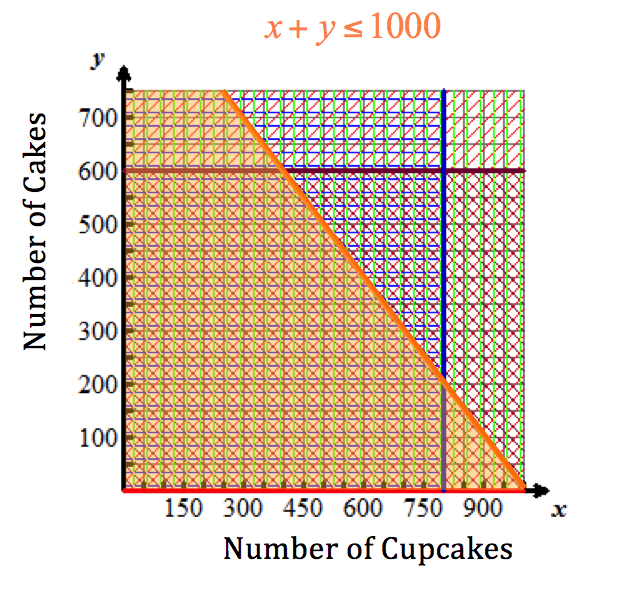
- The inequality x + y ≤ 1000x plus y is less than or equal to 1000 represents the fact that Hermione’s bakery can only hold 1,000 cupcakes and cakes altogether.
- The two conditions x ≥ 0x is greater than or equal to zero and y ≥ 0y is greater than or equal to zero must be included because having negative numbers of cakes and cupcakes is not realistic and does not make sense.
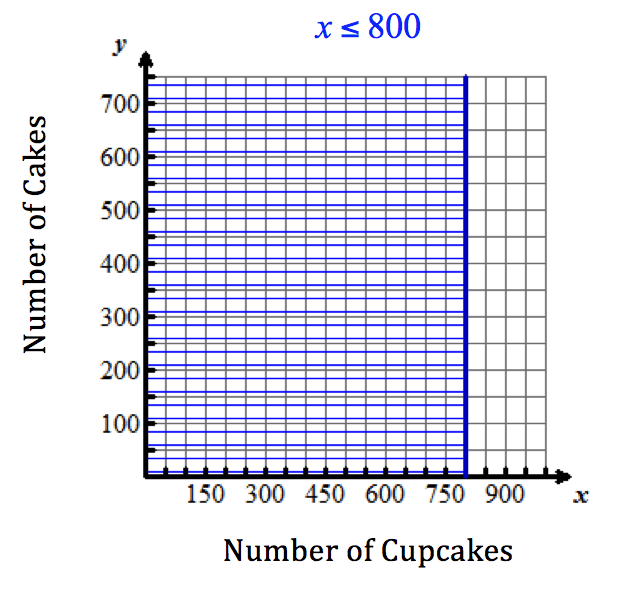
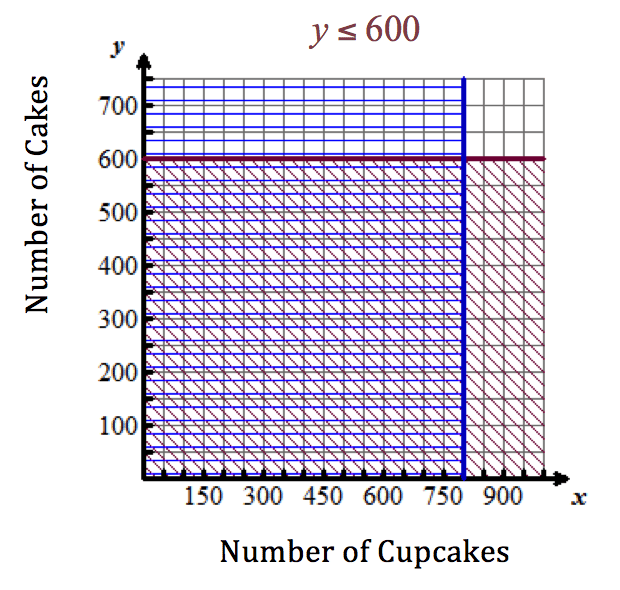
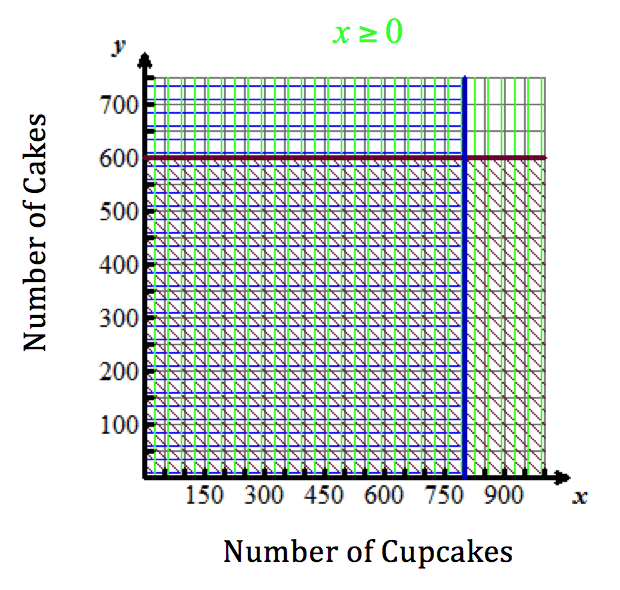
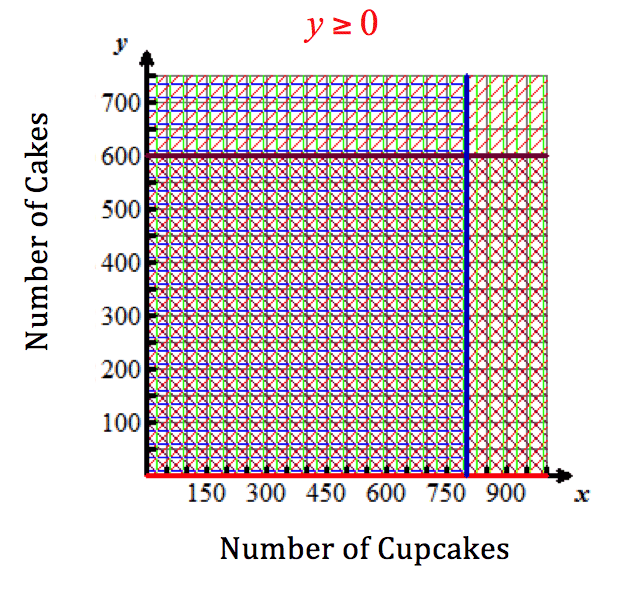
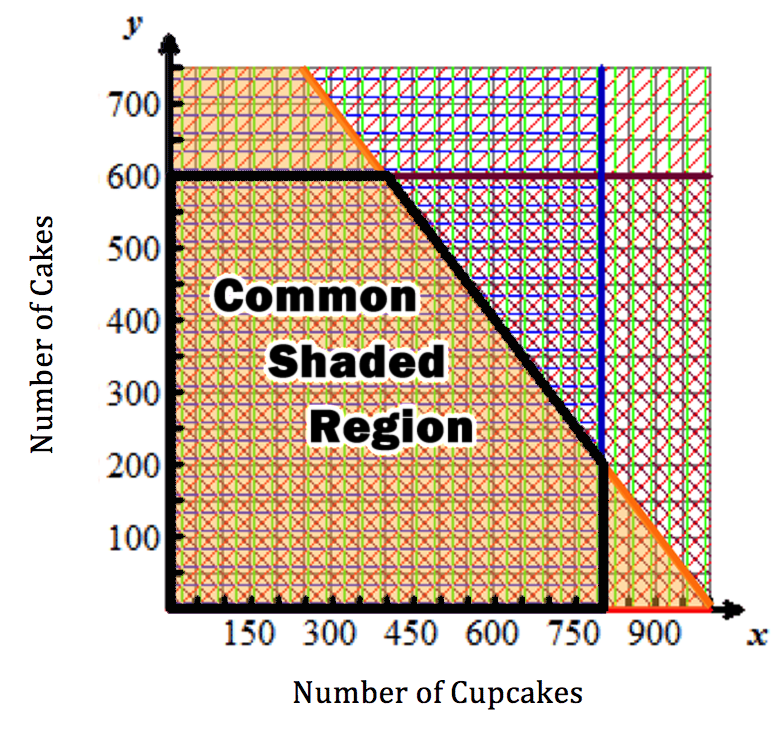
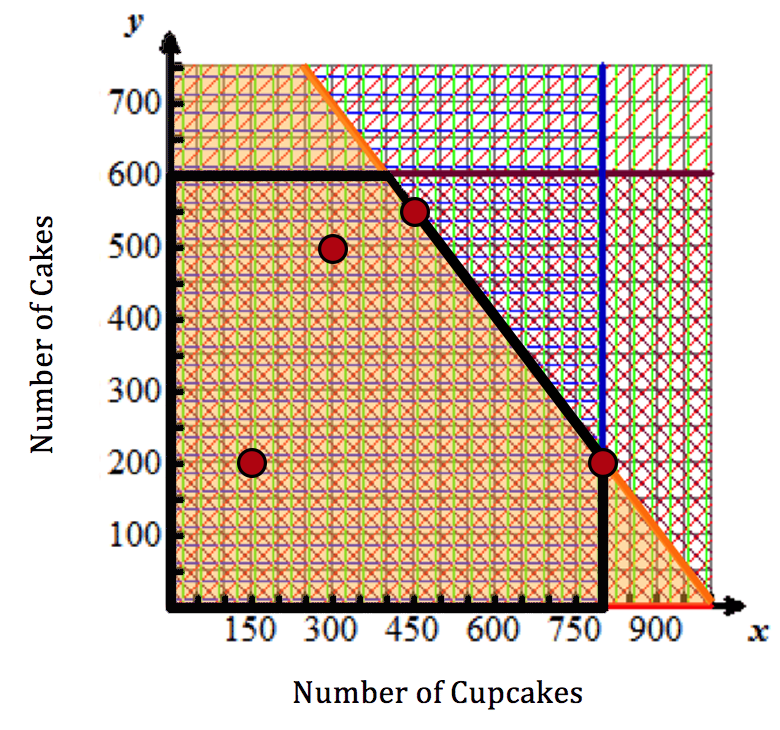
All points in the common shaded region are solutions to the linear inequalities in the situation modeled by this system. Four of these points are shown below in red. Use mental math to check that they are solutions to the equations in the system.
Only certain points in the common shaded region will provide the optimal solution. The optimal solution is the ordered pair (x, y) that produces the highest profit with the objective function:
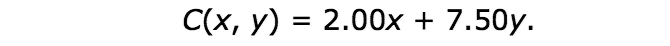
At point (300, 500), Hermione makes $4350. This is found by:
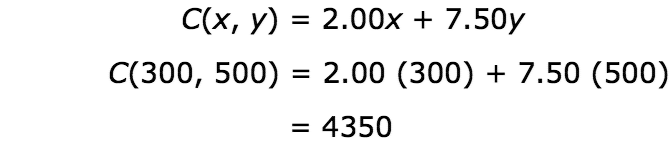
C(300, 500) = 2.00 (300) + 7.50 (500)C of 300 comma 500 equals 2 times 300 plus 7 and five tenths times 500. equals 4350.
At point (800, 200), Hermione makes $3100. This is found by:
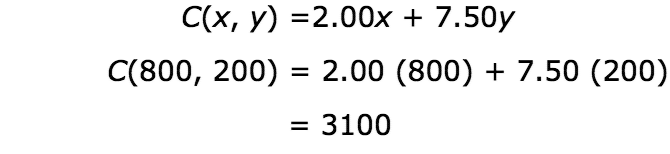
Hermione makes a higher profit selling 300 cupcakes and 500 cakes. (There may be another coordinate pair that produces a higher profit.)
The common shaded area contains many, many possible solutions. Testing all of the points in this region to find which combination of cupcakes and cakes produces the highest profit would be very time consuming!
The vertices of the common shaded region are the points that provide the absolute maximum and minimum solutions to the system of linear inequalities. This is because these points provide the least and greatest values in (x, y) pairs.
The coordinates for the vertices are:
(0, 0), (0, 600), (400, 600), (800, 200) and (800, 0).
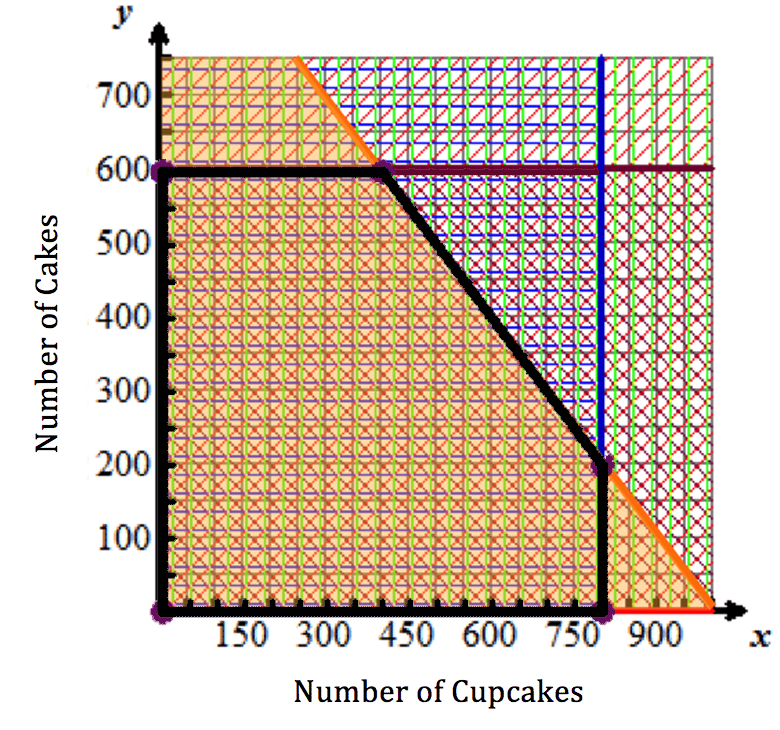
You only need to test the vertices to find which solution set (x, y) will provide the optimal solution. Shown here is the value of the optimizing function, C(x, y) = $2.00x + $7.50y, at each vertex. (Note that vertex (0, 0) is not shown. This point represents not selling any product, and therefore no profit will be made.)

Vertex (0, 600):
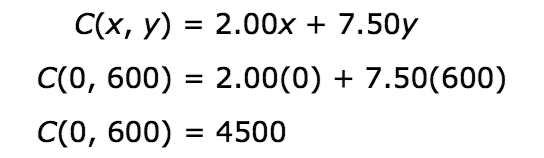
Vertex (400, 600):
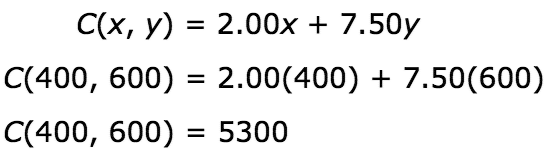
Vertex (800, 200):
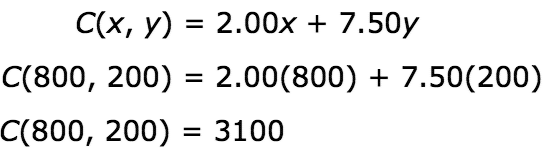
Vertex (800, 0):
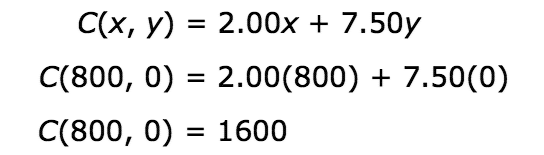
The vertex (400, 600) produced the highest profit for Hermione, which was $5,300. This means Hermione will make the most amount of money when she sells 400 cupcakes and 600 cakes. This combination of 400 cupcakes and 600 cakes also meets the bakery’s production limit of 1,000 cupcakes and cakes per day.
Vertex (400, 600):