Question 1
Perform a regression analysis to determine the curve of best fit for this data. Include a residual plot and the equation for the curve of best fit in your analysis. Describe the curve of best fit and type the equation of the curve of best fit in the space below. (Use the caret, ^ (shift 6), to represent an exponent. For example, 2xtwo to the power of x would be keyed as 2^x)two caret x
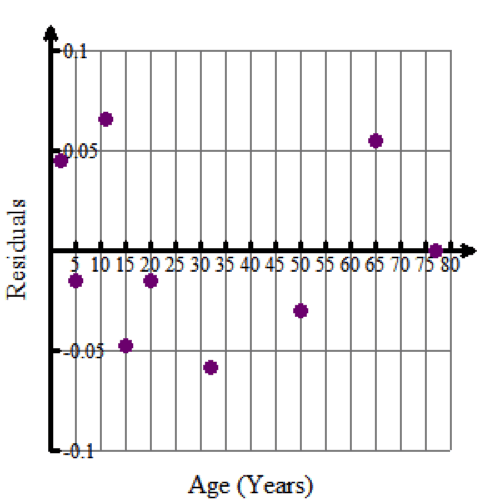
The curve of best fit is an exponential regression curve. Here is the residual plot you should get:
 r = -0.9994
r = -0.9994
R2 = 0.9987 r equals negative nine thousand nine hundred ninety four ten thousandths, and r squared equals nine thousand nine hundred eighty seven ten thousandths.
The exponential regression curve is: y = 100.45(0.9995)xy equals one hundred and forty five hundredths times nine thousand nine hundred ninety five ten thousandths to the power of x., where x is the age (in years) and y is the average temperature (°F)degrees Fahrenheit.
 r = -0.9994
r = -0.9994R2 = 0.9987 r equals negative nine thousand nine hundred ninety four ten thousandths, and r squared equals nine thousand nine hundred eighty seven ten thousandths.
The exponential regression curve is: y = 100.45(0.9995)xy equals one hundred and forty five hundredths times nine thousand nine hundred ninety five ten thousandths to the power of x., where x is the age (in years) and y is the average temperature (°F)degrees Fahrenheit.
Question 2
Determine the average body temperature for your age. Type your answer in the blank.
To determine the average temperature for someone your age, substitute your age in for the value of x. For example, if you are 16:
y = 100.45(0.9995)xy equals one hundred and forty five hundredths times nine thousand nine hundred ninety five ten thousandths to the power of x
y = 100.45(0.9995)16y equals one hundred and forty five hundredths times nine thousand nine hundred ninety five ten thousandths to the power of 16
y = 99.65°Fy equals ninety nine and sixty five degrees Fahrenheit
As an alternate strategy, graph the equation in your graphing calculator. Use the TRACE feature, and find the value of y when x = 16.
y = 100.45(0.9995)xy equals one hundred and forty five hundredths times nine thousand nine hundred ninety five ten thousandths to the power of x
y = 100.45(0.9995)16y equals one hundred and forty five hundredths times nine thousand nine hundred ninety five ten thousandths to the power of 16
y = 99.65°Fy equals ninety nine and sixty five degrees Fahrenheit
As an alternate strategy, graph the equation in your graphing calculator. Use the TRACE feature, and find the value of y when x = 16.