Select an answer from the options below and click Submit.
Use the following scenario to answer Questions 1 and 2.
Question 1
A roller coaster is a perfect example of a real-world object that is designed using piecewise functions.
The beginning of one particular roller coaster design is modeled by the piecewise function given below.
r(x)=
39,0≤x<15
0.04x2−3.6x+84,15≤x<65
12x−272,x≥65
Which graph models the piecewise function r(x)r of x?
r(x)=
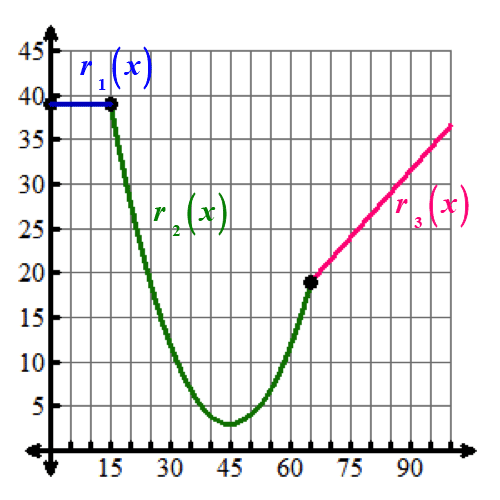
39,0≤x<15
This function, labeled as r1(x), has the value of 39 for all x values less than 15 but great than or equal to 0.
0.04x2−3.6x+84,15≤x<65
This function, labeled as r2(x), is quadratic over the x values less than 65 but great than or equal to 15.
12x−272,x≥65
This function, labeled as r3(x), is linear for all x values greater than or equal to 65.
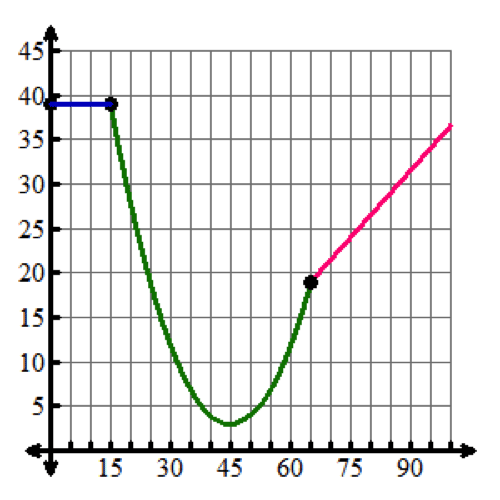
The piecewise function has only solid dots. When x=15, if r2(x)=0.04x2−3.6x+84r sub 2 of x is equal to four hundredths x squared minus three and six tenths x plus 84, then r2(15)=0.04(15)2−3.6(15)+84=39r sub 2 of 15 is equal to four hundredths times 15 squared minus three and six tenths times 15 plus 84 equals 39, and if r1(x)=39r sub 1 of x equals 39, then r1(15)=39r sub 1 of 15 equals 39 also equals 39. The piecewise function connects at the point (15, 39). This same connection happens when x=65 because r2(65)=19r sub 2 of 65 equals 19 and r3(65)=19r sub 3 of 65 equals 19.
Go to question 2.
Question 2
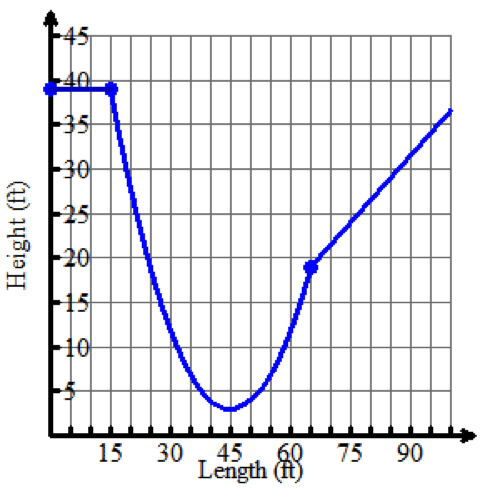
r(x)=
39,0≤x<15
0.04x2−3.6x+84,15≤x<65
12x−272,x≥65
What is the average rate of change of the roller coaster’s height with respect to length from its initial drop-off at x=15 to when the path becomes linear at x=65?
r(x2)−r(x1)x2−x1=r(65)−r(15)65−15=19−3965−15=-negative2050=-negative25 the difference between r of x sub 2 and r of x sub 1 divided by the difference between x sub 2 and x sub 1equals the difference between r of 65 and r of 15 divided by the difference between 65 and 15 equals the difference between 19 and 39 divided by the difference between 65 and 15 equals negative twenty divided by fifty equals negative two fifths.
Note that there are no units included in this rate of change. This is because the rate of change is -negative2ft5ftnegative two feet divided by five feet, which means a vertical change of two feet for every horizontal change of five feet. The unit ‘feet’ divides out, since it is in both the numerator and the denominator. Go to question 3.
r(x2)−r(x1)x2−x1 the difference between r of x sub 2 and r of x sub 1 divided by the difference between x sub 2 and x sub 1
Use the following scenario to answer Questions 3 and 4.
Question 3
A common real-world application of step functions is the United States Postal Service (USPS). The USPS charges flat rates depending on the weight of packages.
The step function below shows the cost to ship packages at various weights.
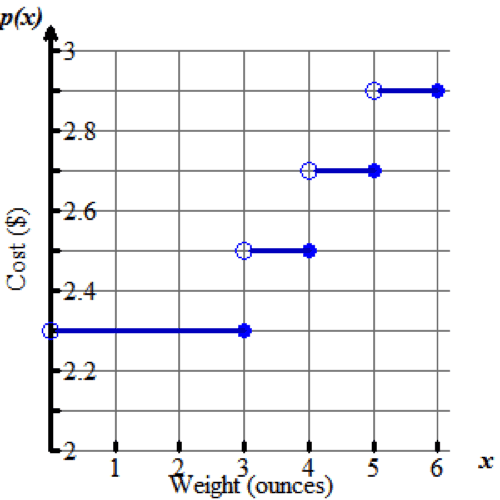
Select the algebraic representation that models the step function shown.
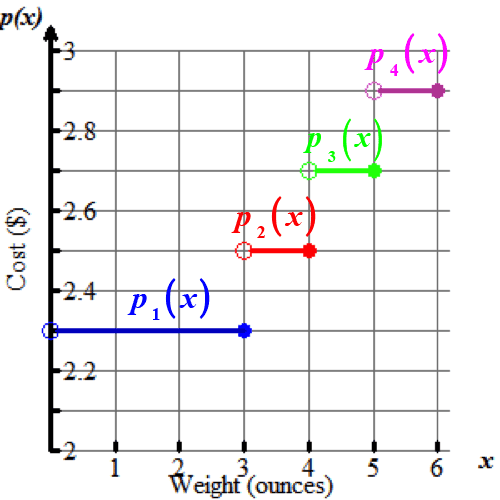
p(x)=
$2.30,x≤3
$2.50,3<x≤4
$2.70,4<x≤5
$2.90,5<x≤6
Go to question 4.
Question 4
p(x)=
$2.30,x≤3
$2.50,3<x≤4
$2.70,4<x≤5
$2.90,5<x≤6
How much more does a person pay to ship a package that weighs 5.2 ounces versus a package that weighs 3.8 ounces?
Use the following scenario to answer Questions 5 and 6.
Question 5
Have you ever played with a laser beam, been to a laser show, or seen a teacher use a laser pointer? Laser beams have very interesting properties.
For example, when you point a laser beam at a mirror, the beam reflects back at exactly the same angle to which the beam is pointing.
The graph below models the beam of a laser. The laser pointer is positioned at x=0. The beam is reflected off of a mirror positioned at 3≤x≤7x is greater than or equal to 3 but less than or equal to 7. The path of the beam resembles a piecewise function.
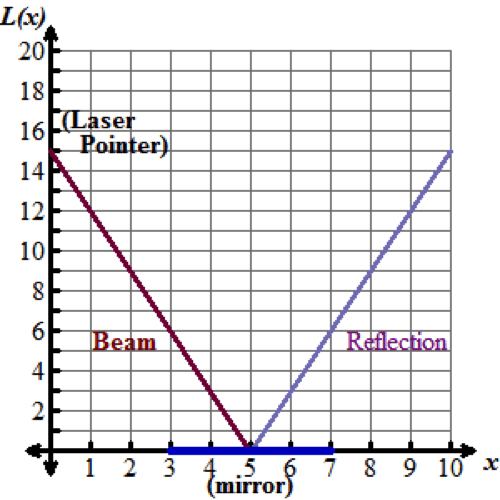
A portion of the algebraic representation for the laser’s piecewise function, L(x)L of x, is given below. Select the completed function that shows the appropriate domain for L(x)L of x so that it models the laser beam.
L(x)=
-negative3x+15,
3x−15,
L(x)=
-negative3x+15,0≤x<5
This function models the beam from the pointer to the mirror.
3x−15,x≥5
This function models the reflected beam, from the mirror out to space.
Go to question 6.
Question 6
The piecewise function L(x)=
-negative3x+15,0≤x<5
3x−15,x≥5
When the two linear functions are pieced together over the domain 0≤x<5x greater than or equal to 0 but less than 5 and x≥5x greater than or equal to 5, respectively, what new function family is represented?